The reflectance of light hitting a dielectric (non-metal) / dielectric interface is something commonly needed in computer graphics, and one of the few material properties that we can get a compact and exact solution for, from Maxwell's equations.

In computer graphics, a faster approximation is often used - Schlick's approximation. It kind of sucks tho - it has quite large relative error, resulting in visibly incorrect reflection.

For the n_1 = 1, n_2 = 1.5 case, the relative error is 23.2%, and for n_2=1.333, the relative error is 32.5% !

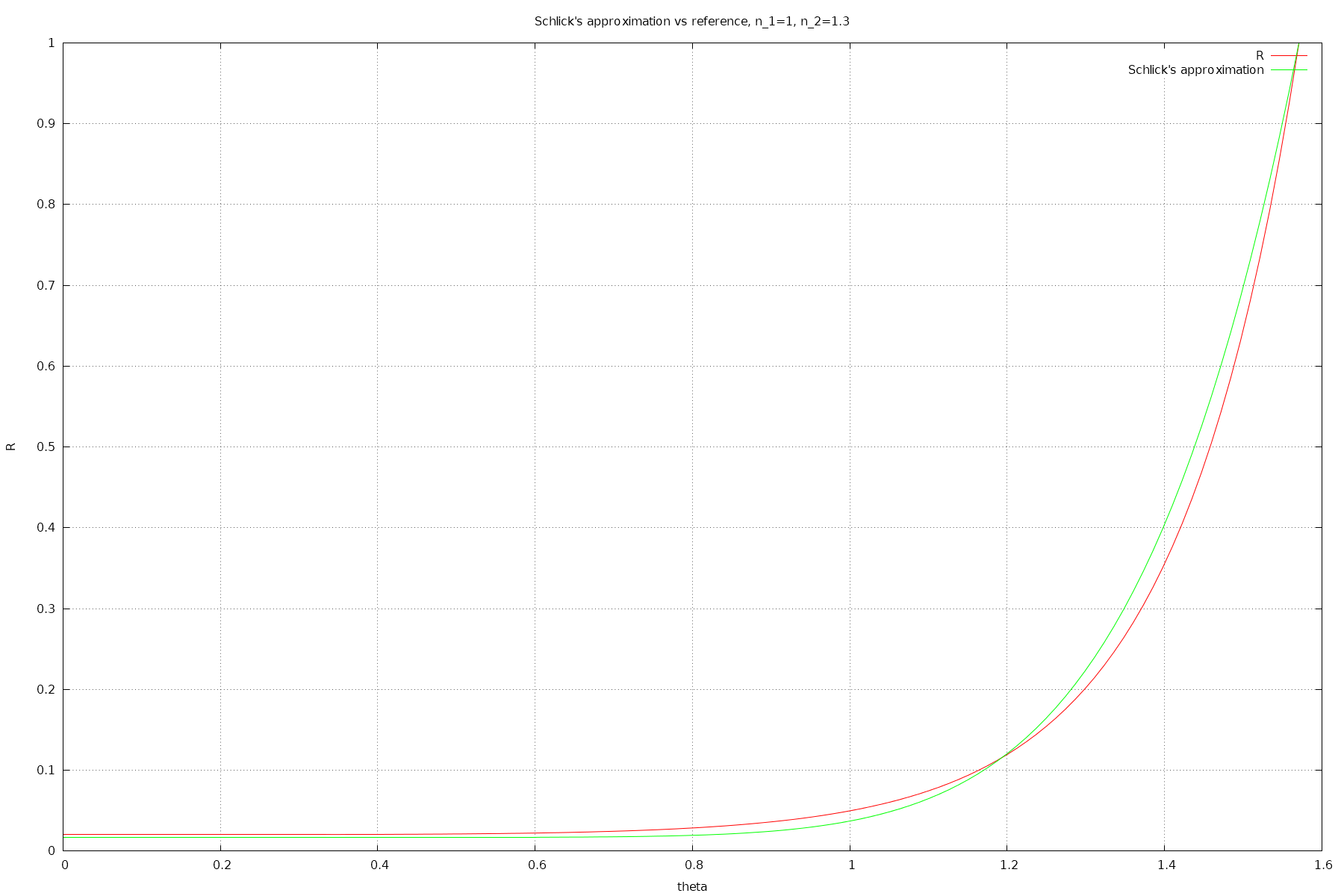Schlick's approximation for n_2=1.3

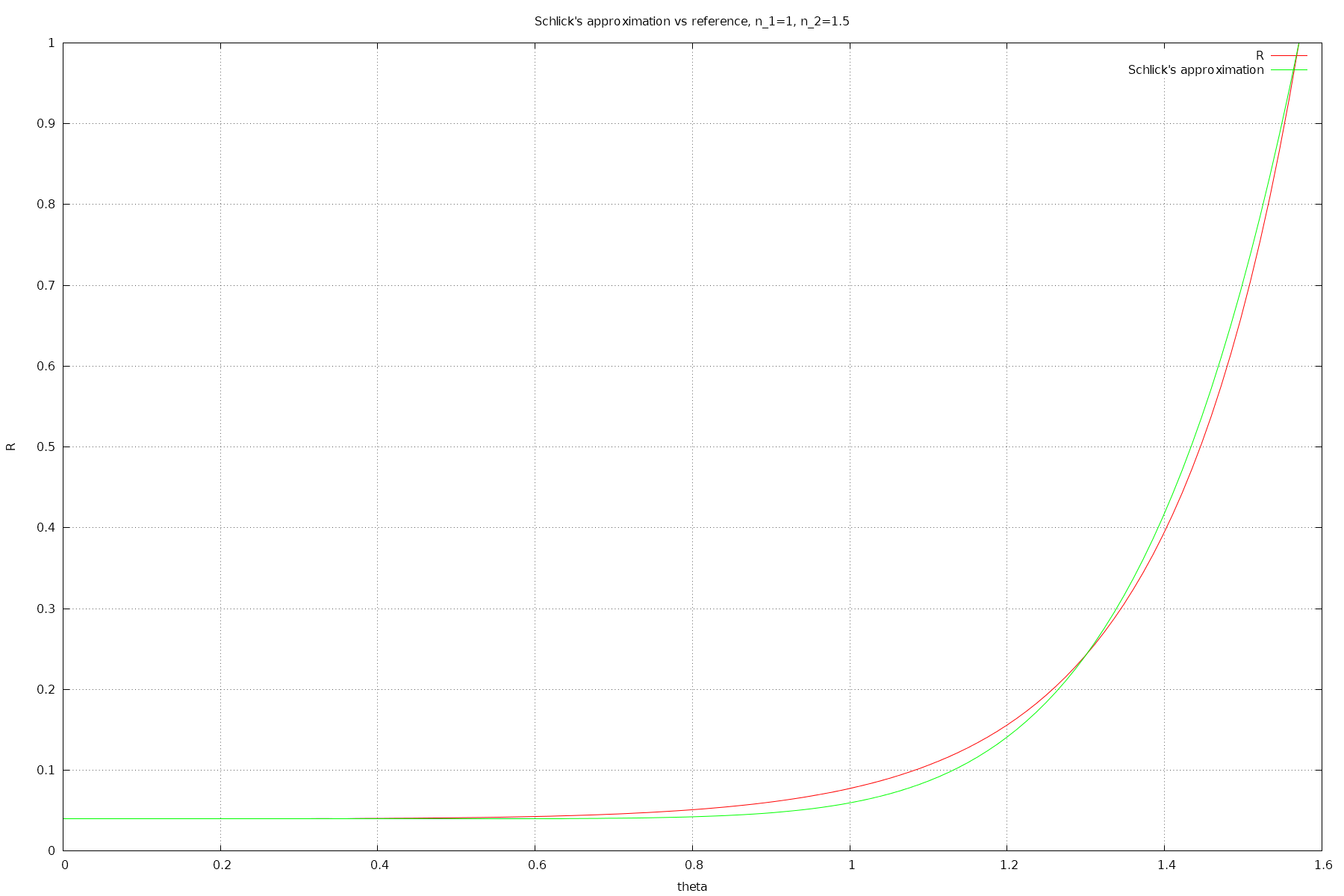Schlick's approximation for n_2=1.5

This has been bugging me for a while (a decade plus), so while fixing some NaNs I decided I should yak shave and look into it - can I do better?

It's hard to come up with a simple formula that can handle a range of IORs, but if you assume a fixed IOR, you can get some nice results.

These approximations are useful for applications like computer games, where all shaders may use a few fixed IOR values. For example your water shader will probably always have IOR 1.333.

For n_2=1.333 (the IOR of water):

float dielectricFresnelReflForIOR1_333(float cos_theta_i)
{
	const float cos_theta_2 = cos_theta_i*cos_theta_i;
	return 
		(1.1040283f*cos_theta_2 + -1.6791086f*cos_theta_i + 0.86057293f) /
		(9.739124f *cos_theta_2 + 3.293334f  *cos_theta_i + 0.8676968f);
}

And a plot of it: 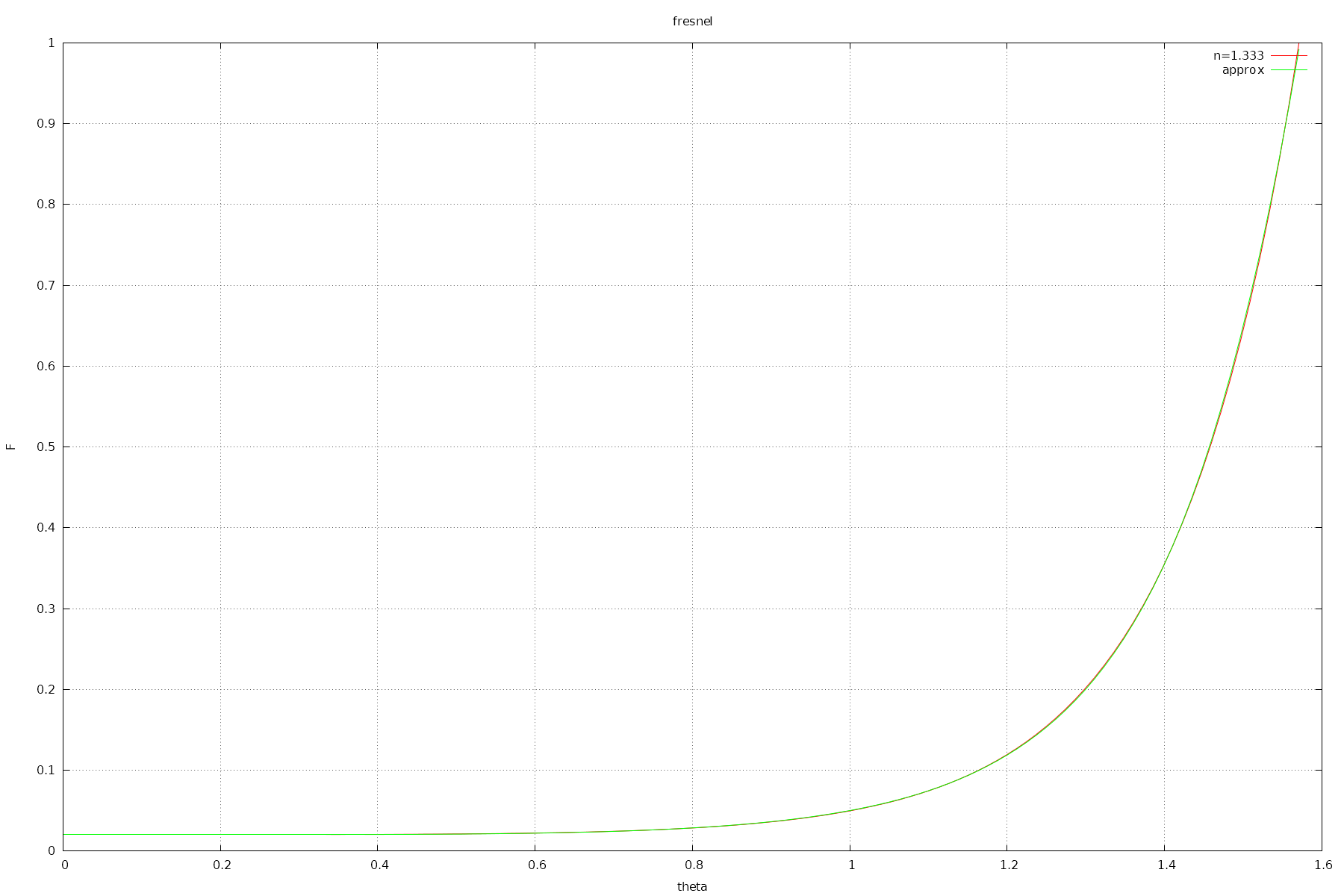dielectricFresnelReflForIOR1_333 vs reference

It has relative and absolute error <= 0.00821. (0.8%)

For n_2=1.5 (approximately glass, plastic):

float dielectricFresnelReflForIOR1_5(float cos_theta_i)
{
	const float cos_theta_2 = cos_theta_i*cos_theta_i;
	return 
		(-2.4615278f*cos_theta_2 +  3.473652f*cos_theta_i + -1.9117112f) /
		(-13.303401f*cos_theta_2 + -7.186081f*cos_theta_i + -1.9189386f);
}

And a plot of it:

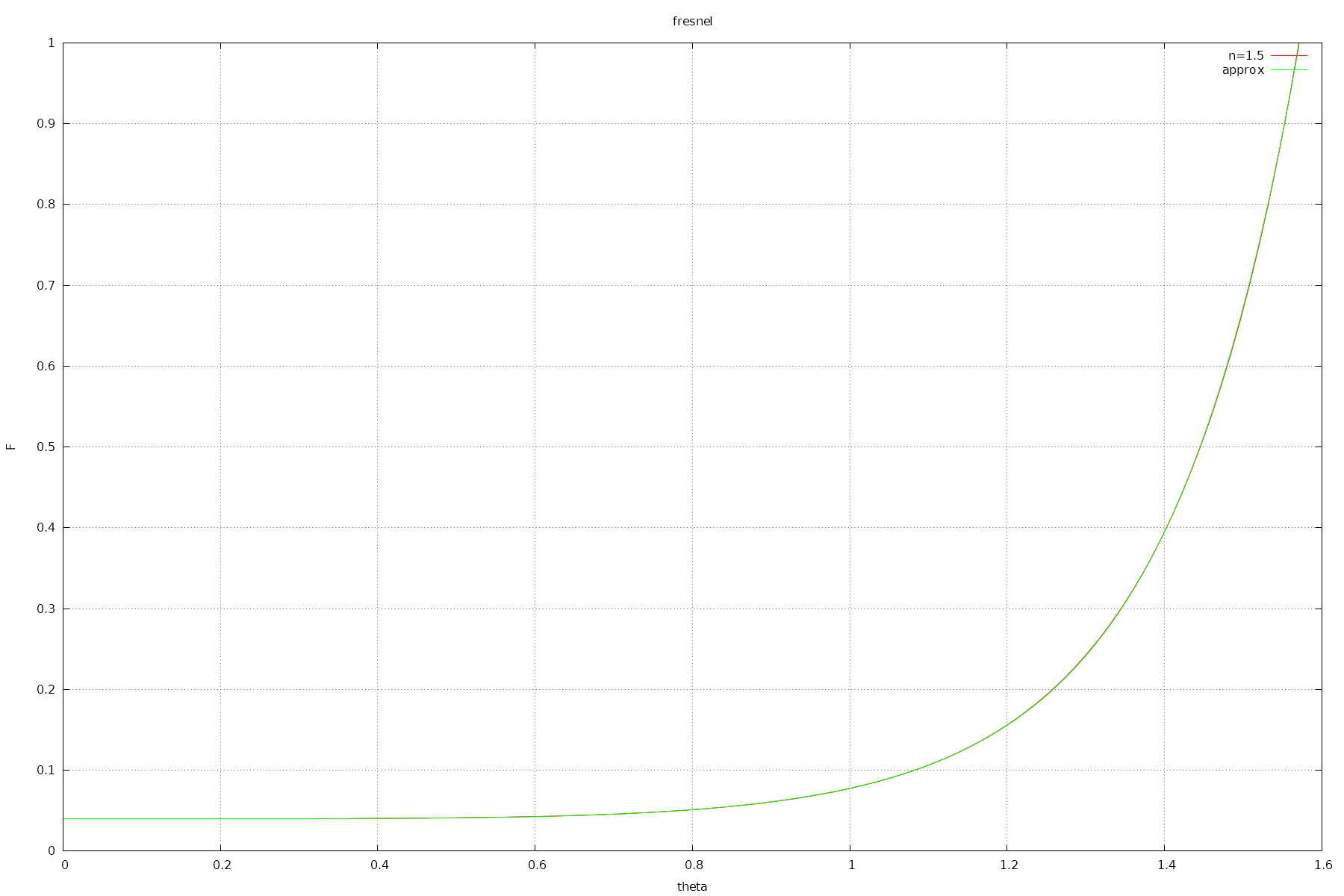dielectricFresnelReflForIOR1_5 vs reference

It has relative and absolute error <= 0.00382. (0.3%)

As you can see, these approximations are much more accurate than Schlick's.

What's the performance like? These functions run in around 23 cycles on my Zen 3 CPU machine. This is significantly faster than the exact Fresnel reflectance code which runs in around 54 cycles.

I used a rational function (a ratio of two quadratic polynomials) as the approximating functions - I think rational functions are pretty cool - they can fit curves polynomials can't with very few parameters. I used a custom search program to find the coefficients.

I also did a program search for a formula that can approximate the Fresnel reflectance curve for a range of IORs, and found something - but it's not that much faster than the exact code, so not sure it's worth using.