Fast acos approximation
Continuing with the theme of fast function approximations (see the previous post on Fresnel curve approximations), using my custom program search algorithm, I have come up with a fast approximate acos (arccosine) function.
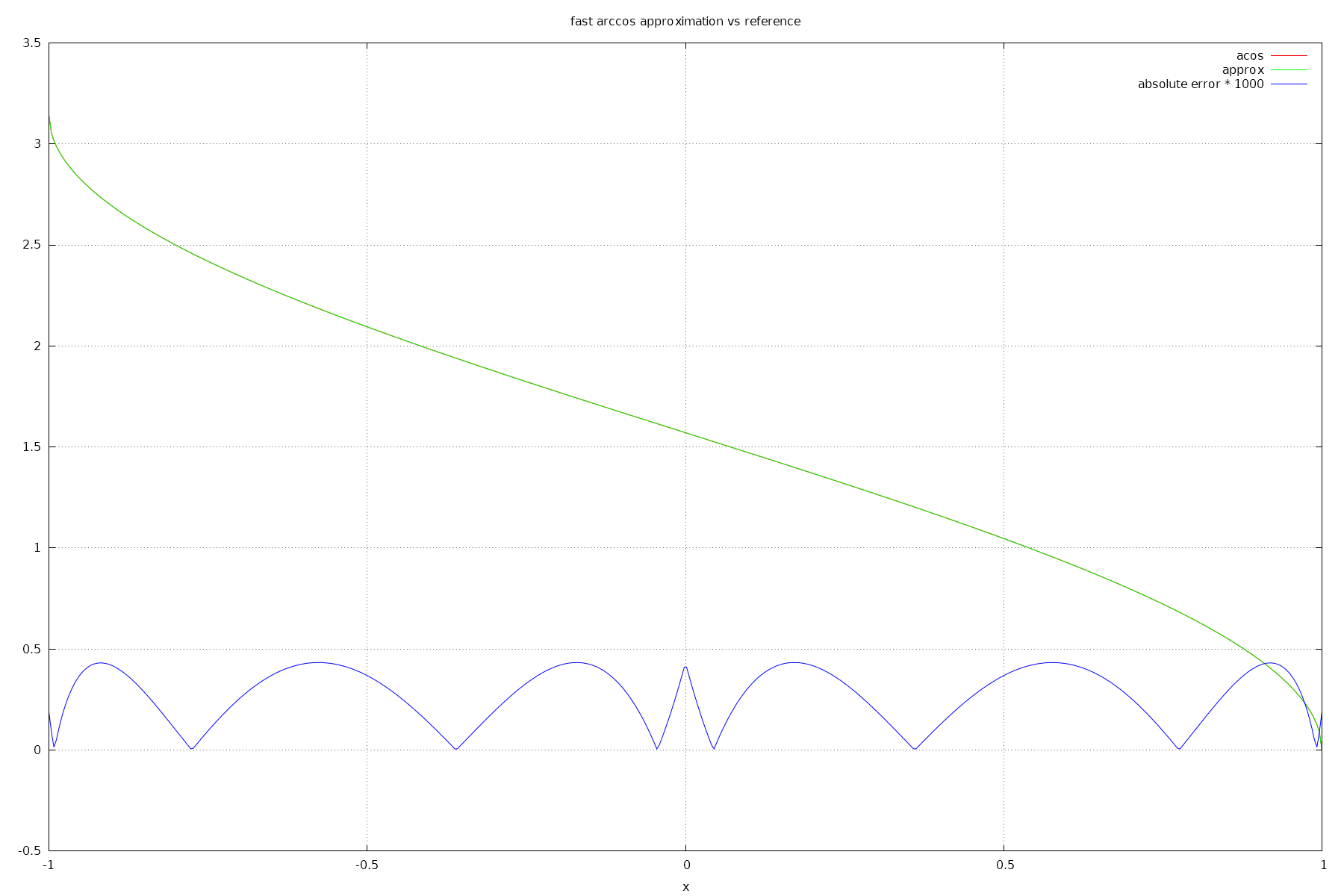
Absolute error is <= 0.0004333.
The idea for the sqrt(2 - 2x) comes from Trey Reynolds
// Code by Nicholas Chapman
static float fastApproxACos(float x)
{
if(x < 0.f)
return 3.14159265f - ((x * 0.124605335f + 0.1570634f) * (0.99418175f + x) + sqrt(2.f + 2.f * x));
else
return (x * -0.124605335f + 0.1570634f) * (0.99418175f - x) + sqrt(2.f - 2.f * x);
}
Timings:
On my AMD 5900X CPU:
std::acos(float) took 11.698 ns / iter (~55 cycles) fastApproxACos took 5.7512 ns / iter (~27 cycles)
So it's about twice as fast as the C++ standard library single-precision acos.
It's also significantly faster than GLSL's acos on my GPU (RTX 3080).
Here's a plot of it:
Note that on this plot, the acos and fastApproxACos curves are indistinguishable (lie on the same pixels).
EDIT: replaced fastApproxACos code with a slightly simpler expression in the first branch.